What is the fraction for the following decimal expansion? This question delves into the fascinating world of rational numbers and their decimal representations. Understanding the conversion between decimals and fractions is crucial in various mathematical applications, from solving equations to calculating measurements.
In this exploration, we will uncover the methods for converting both terminating and non-terminating decimals into their corresponding fractions, examining special cases where decimal expansions may not represent rational numbers.
Decimal expansions provide a convenient way to represent rational numbers, allowing us to express them as a sequence of digits. However, to perform certain mathematical operations or to gain a deeper understanding of the number’s properties, it often becomes necessary to convert the decimal expansion back into its fractional form.
This process involves identifying the relationship between the decimal digits and the place values they occupy, enabling us to construct an equivalent fraction that accurately represents the original decimal.
What is the Fraction for the Following Decimal Expansion?

In mathematics, a decimal expansion is a way of representing rational numbers using a base-10 number system. It involves expressing the number as a sum of powers of 10, with each power multiplied by a digit from 0 to 9.
Converting Decimals to Fractions: What Is The Fraction For The Following Decimal Expansion
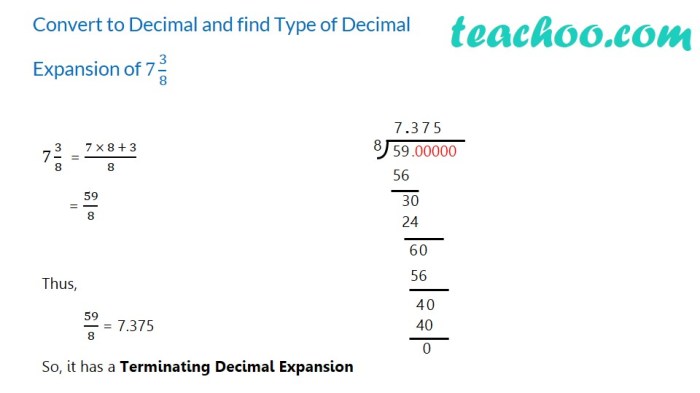
To convert a terminating decimal expansion to a fraction, we can use the following steps:
- Multiply the decimal by an appropriate power of 10 to eliminate the decimal point.
- Express the resulting number as a fraction with the denominator equal to the power of 10 used in step 1.
For example, to convert the decimal 0.5 to a fraction, we can multiply it by 10 to get 5, and then express 5 as the fraction 5/10, which can be simplified to 1/2.
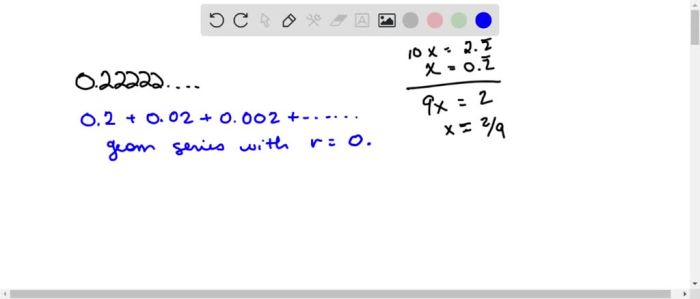
Handling Non-Terminating Decimals, What is the fraction for the following decimal expansion
Non-terminating decimals are decimals that do not end or repeat. They can be classified into two types:
- Terminating decimals:Decimals that eventually end.
- Non-terminating, non-repeating decimals:Decimals that never end and do not repeat any pattern of digits.
Terminating decimals can be converted to fractions using the method described in the previous section. Non-terminating, non-repeating decimals, however, cannot be expressed as fractions because they do not represent rational numbers.
Special Cases
There are some special cases where the decimal expansion of a number may not represent a rational number. These include:
- Irrational numbers:Numbers that cannot be expressed as a fraction of two integers. Examples of irrational numbers include π and √2.
- Decimals that represent repeating fractions:Decimals that have a repeating pattern of digits. These decimals can be expressed as fractions using methods like long division.
Essential Questionnaire
What is a decimal expansion?
A decimal expansion is a representation of a rational number as a sequence of digits to the right of a decimal point.
How do I convert a terminating decimal to a fraction?
To convert a terminating decimal to a fraction, multiply the decimal by an appropriate power of 10 to eliminate the decimal point, and then write the resulting number as a fraction with a denominator equal to the power of 10 used.
How do I convert a non-terminating decimal to a fraction?
To convert a non-terminating decimal to a fraction, identify the repeating block of digits and use long division to find the fraction that generates the repeating block.