Identify the function family to which f belongs – Identifying the function family to which f belongs is a crucial step in understanding its behavior and properties. Function families are groups of functions that share common characteristics, such as their algebraic form, graph shape, or asymptotic behavior. By recognizing the function family, we can leverage our knowledge of its general properties to analyze and solve problems involving that function.
To identify the function family of a given function f, we need to examine its key characteristics, such as its degree, leading coefficient, and presence of any transformations. Based on these characteristics, we can determine which function family f belongs to, such as linear, quadratic, exponential, logarithmic, or trigonometric functions.
1. Definition of Function Family

A function family is a set of functions that share common characteristics. Each member of the family is defined by a specific formula or equation, but they all exhibit similar behavior or properties.
Common examples of function families include linear functions, quadratic functions, exponential functions, and trigonometric functions.
2. Identifying Function Family Membership: Identify The Function Family To Which F Belongs
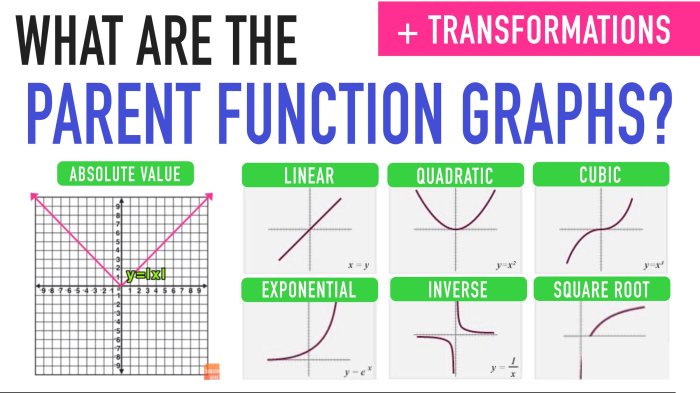
To determine which function family a given function belongs to, examine its key characteristics. These characteristics may include:
- The type of variables involved (e.g., real numbers, complex numbers)
- The shape of the graph (e.g., linear, parabolic, exponential)
- The domain and range of the function
- The presence of specific terms or operations (e.g., exponents, trigonometric functions)
3. Methods for Function Family Identification
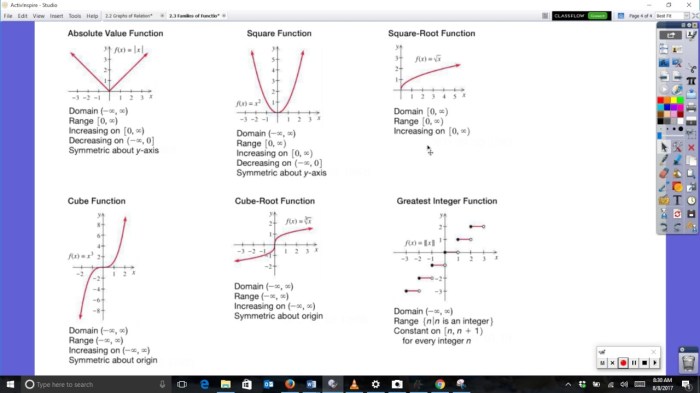
There are several methods for identifying the function family of a given function:
- Visual Inspection:Examine the graph of the function to determine its shape and characteristics.
- Algebraic Analysis:Analyze the function’s equation to identify specific terms or operations that indicate a particular function family.
- Comparison to Known Functions:Compare the given function to known functions from common function families to identify similarities.
4. Examples of Function Family Identification
| Function | Function Family | Reasoning |
|---|---|---|
| y = 2x + 1 | Linear | Constant slope, linear graph |
| y = x^2 | Quadratic | Parabolic graph, exponent of 2 |
| y = e^x | Exponential | Exponential function with base e |
| y = sin(x) | Trigonometric | Sine function, periodic graph |
5. Applications of Function Family Identification
Identifying function families has practical applications in mathematical analysis and problem-solving. It allows us to:
- Predict the behavior of functions
- Classify and organize functions
- Solve equations and inequalities
- Model real-world phenomena
FAQ Guide
What are the key characteristics that define each function family?
Each function family has unique characteristics, such as degree, leading coefficient, and asymptotic behavior. For example, linear functions have a degree of 1, quadratic functions have a degree of 2, exponential functions have a constant base raised to a variable exponent, and trigonometric functions involve periodic oscillations.
How do we determine which function family a given function belongs to?
To determine the function family of a given function f, we examine its algebraic form and key characteristics. We look for patterns, such as constant terms, coefficients, exponents, and transformations. By comparing these characteristics to the known properties of different function families, we can identify the family to which f belongs.